3D illustrations to Chapter 8 of Cromwell's Polyhedra

Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25 , 1000 Ljubljana , Slovenia
e-mail: izidor.hafner@fe.uni-lj.si

One way to improve teaching of stereometry is to give 3D illustrations to well known textbooks. As an example let us take Chapter 8 of Cromwell's Polyhedra. Chapter 8 is dealing with symmetry.

Systems of rotational symmetry Cyclic symmetry

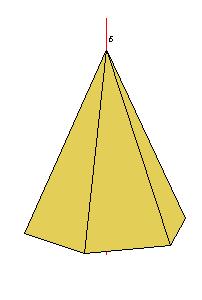
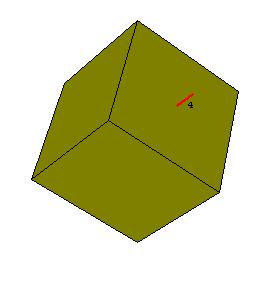
Figure 8.1. A rotation axis in a cyclic system

Dihedral symmetry

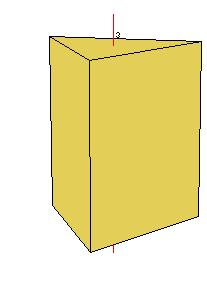
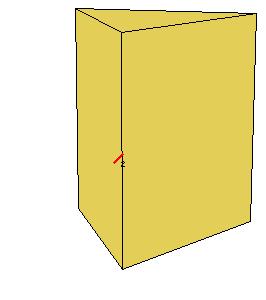
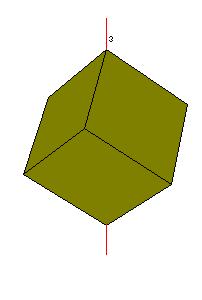
Figure 8.2. Principal and secondary axes in a dihedral system

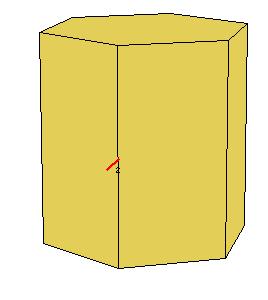
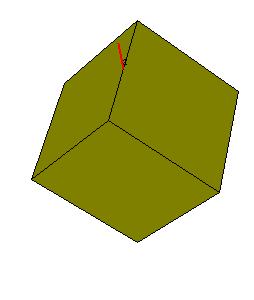
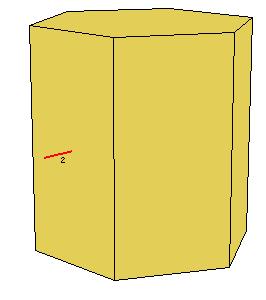
Figure 8.3. When n is even, the secondary axes in Dn can be separated into two kinds

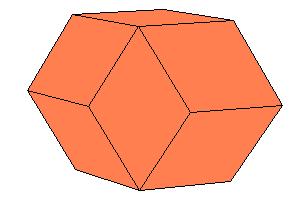
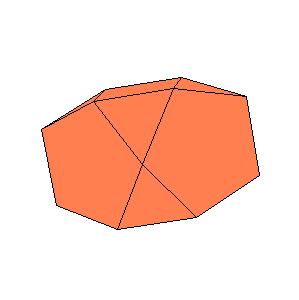
Figure 8.4. Polyhedra with D2 symmetry.

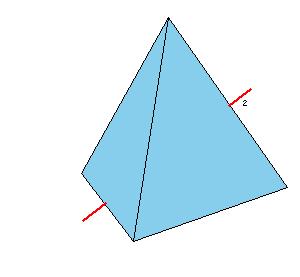
Tetrahedral symmetry

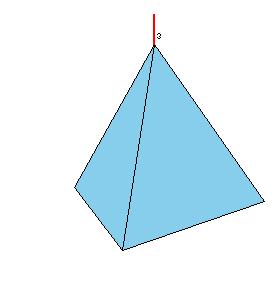
Figure 8.5. Rotation axes in the tetrahedral system.

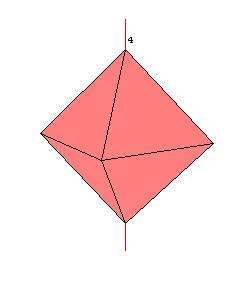
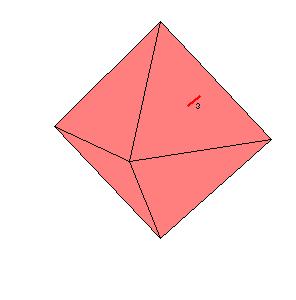
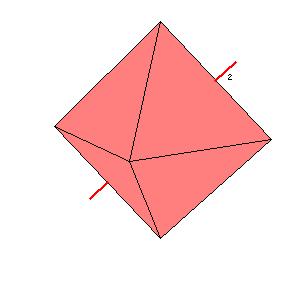
Octahedral symmetry

Figure 8.6. Rotation axes in the octahedral system.

Icosahedral Symmetry

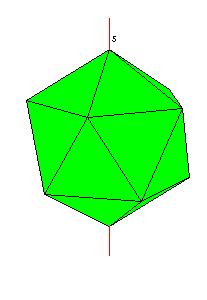
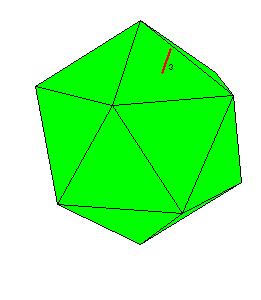
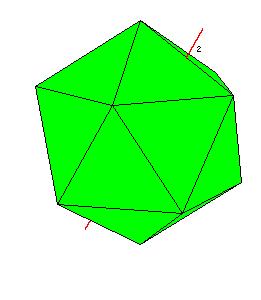
Figure 8.7. Rotation axes in the icosahedral system.

Reflection symmetry

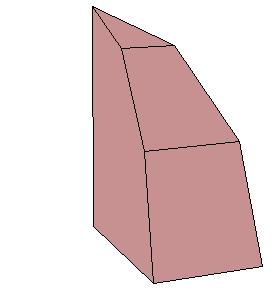
Figure 8.9. A polyhedron with bilateral symmetry.

Prismatic symmetry types

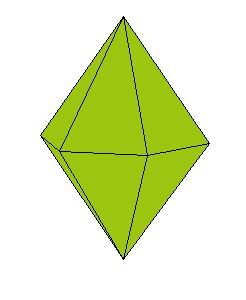
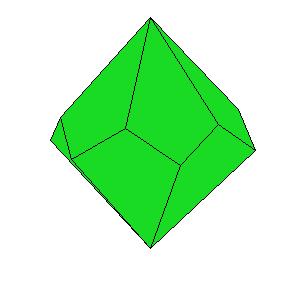
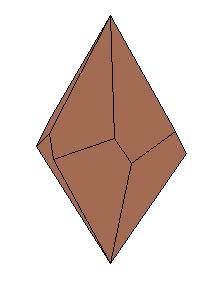
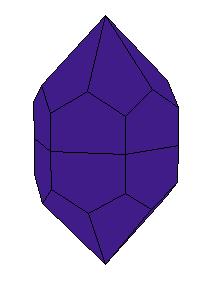
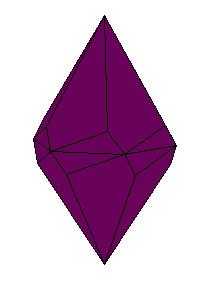
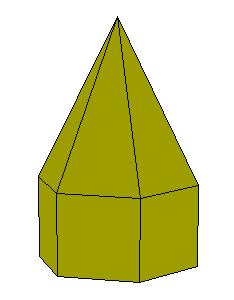
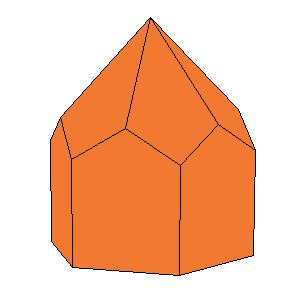
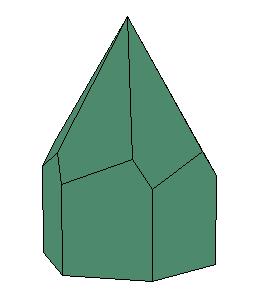
Figure 8.10. Polyhedra with prismatic symmetry.

Symmetry type Dnh.

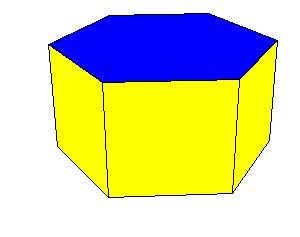
Figure 8.11.

Symmetry type Dnv.

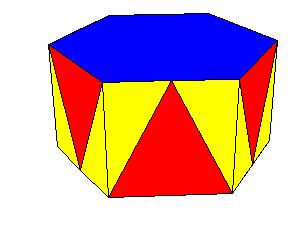
Figure 8.12.

Symmetry type Dn.

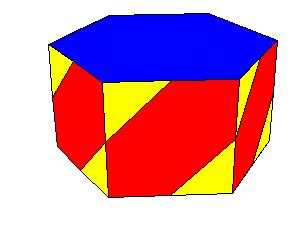
Figure 8.13.

Symmetry type Cnv

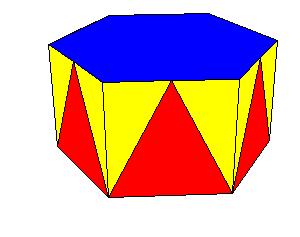
Figure 8.14.

Symmetry type Cnh

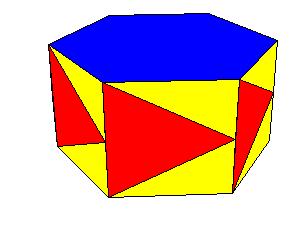
Figure 8.15.

Symmetry type Cn.

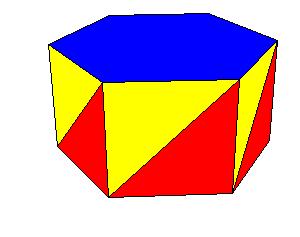
Figure 8.16.

Compound symmetry and the S2n symmetry type

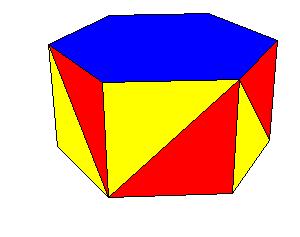
Figure 8.17.

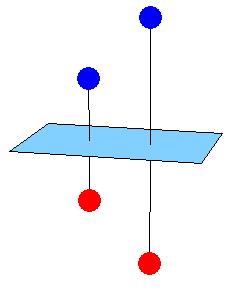
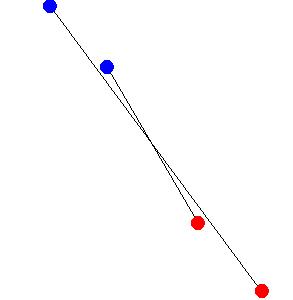
reflection in a plane reflection in a point
Figure 8.20.

Cubic symmetry types
Symmetry type Oh.

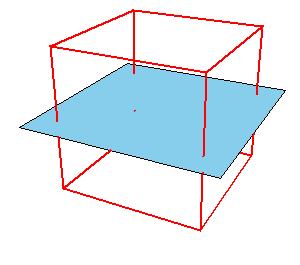
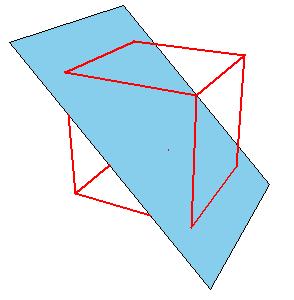
Figure 8.21. The reflection planes of a cube.

Symmetry type O

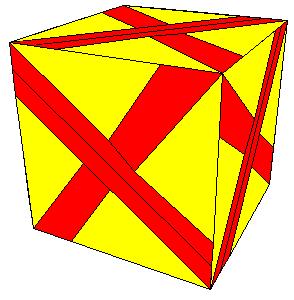
Figure 8.22.

Symmetry type Th.

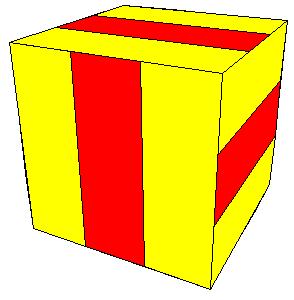
Figure 8.23.

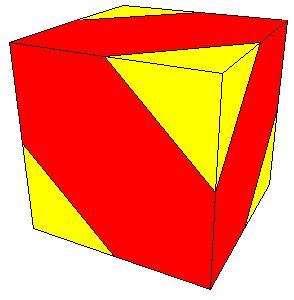
Figure 8.25.

Symmetry type T

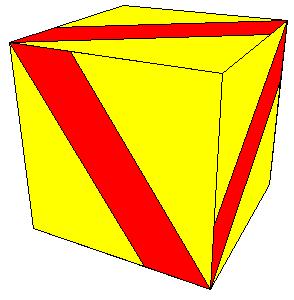
Figure 8.26.

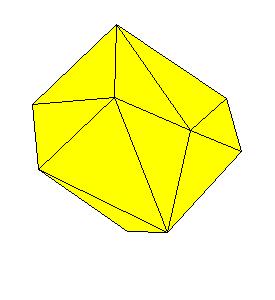
Figure 2.27.

Some examples

The cube has octahedral rotational symmetry.

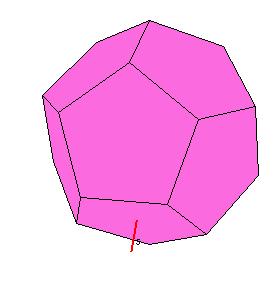
The dodecahedron has icosahedral rotational symmetry.

We get examples of tetrahedral symmetry by colouring polyhedra with octahedral and icosahedral symmetry.

References

[1] P. R. Cromwell, Polyhedra, Cambridge University Press 1997.
[2] Martin Kraus' Live3D applet