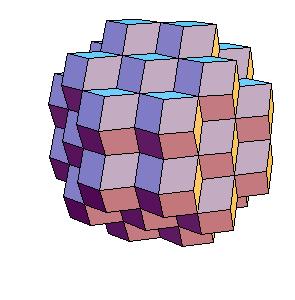
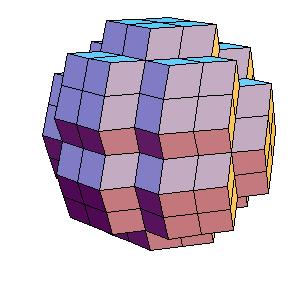
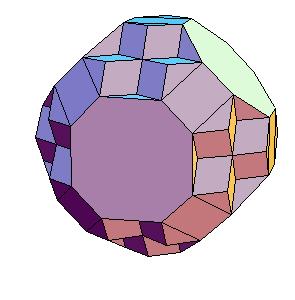
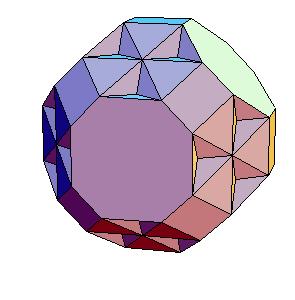
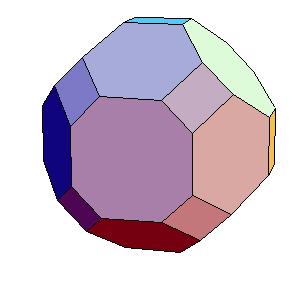
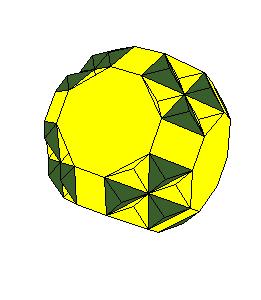
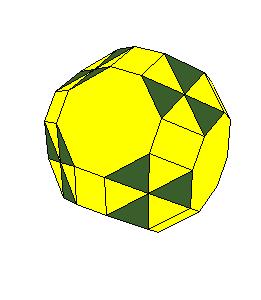
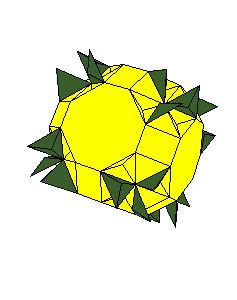
Hinged dissection of a rhombic solid to the truncated cuboctahedron
Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25
, 1000 Ljubljana
, Slovenia
e-mail: izidor.hafner@fe.uni-lj.si
It is well known that truncated cuboctaheda fill the space together with octagonal prisms
[4, pg. 181].
The fact that it is possible to dissect the truncated cuboctahedron to a cube follows from [1, pg. 331].
Results of dissections from the truncated cuboctahedon are not mentioned in [2,3], where many dissections from truncated octahedron are given.
Here we present a hinged dissection of a "rhombic solid" to the truncated cuboctahedron.
By "rhombic solid" we mean a solid composed of
rhombic dodecahedra (including the case of using halves of rhombic dodecahedron and 1/6 or 1/12 of a cube).
Our truncated cuboctahedron is not Archimedean but can be enlarged to one using additional prisms.
References
[1] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are
rational, Discrete & Computational Geometry, 22 (1999), pages 321-332.
[2] G. N. Frederickson, Dissections: Plane & Fancy, Cambridge U. Press, 1997.
[3] G. N. Frederickson, Hinged Dissections:Swinging & Twisting, Cambridge U. Press, 2002.
[4] R. Williams, The Geometrical Foundation Of Natural Structure, Dover 1972
[5] I. Hafner, T. Zitko, Dissection of rhombic 36-hedron to a tetrahedron and a truncated
tetrahedron
[6] I. Hafner, T. Zitko, Hinged dissection of a rhombic solid to the truncated octahedron