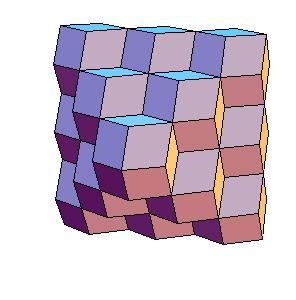
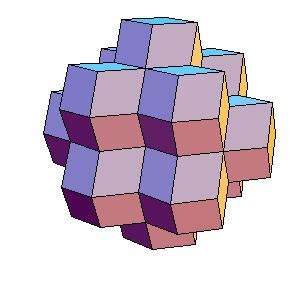
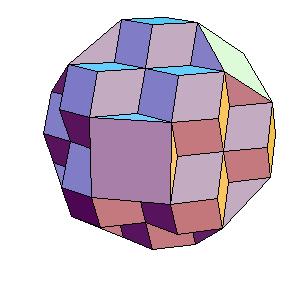
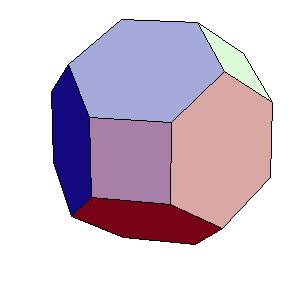
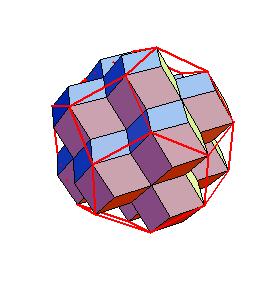
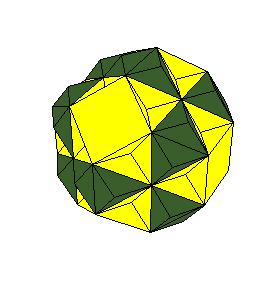
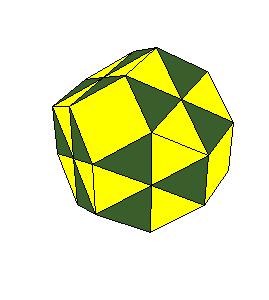
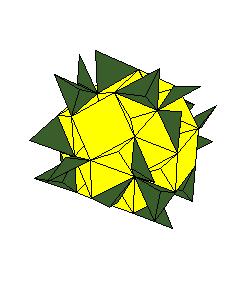
Hinged dissection of a rhombic solid to the truncated octahedron
Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25
, 1000 Ljubljana
, Slovenia
e-mail: izidor.hafner@fe.uni-lj.si
It is well known fact that truncated octaheda fill the space [4, pg. 167].
That it is possible to dissect the truncated octahedron to a cube follows also from [1, pg. 331].
There are known results of dissections from the truncated octahedra [3, pg. 200-205],
among them is also its dissection to a cube.
Here we present a hinged dissection of a rhombic solid to the truncated octahedron.
By "rhombic solid" we mean a solid composed of
rhombic dodecahedra (including the case of using halves of rhombic dodecahedron).
Our rhombic solid is obtained by putting 12 rhombic dodecahedra, one on
each face of a given rhombic dodecahedron and then put additional 6 halves of
dodecahedron at axes of four-fold symmetry.
So the rhombic solid is composed of 16 rhombic
dodecahedra.
References
[1] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are
rational, Discrete & Computational Geometry, 22 (1999), pages 321-332.
[2] G. N. Frederickson, Dissections: Plane & Fancy, Cambridge U. Press, 1997.
[3] G. N. Frederickson, Hinged Dissections:Swinging & Twisting, Cambridge U. Press, 2002.
[4] R. Williams, The Geometrical Foundation Of Natural Structure, Dover 1972
[5] I. Hafner, T. Zitko, Dissection of rhombic 36-hedron to a tetrahedron and a truncated tetrahedron