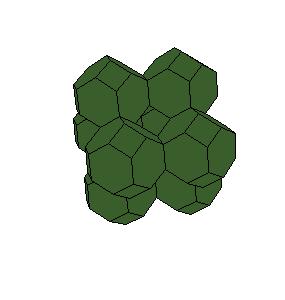
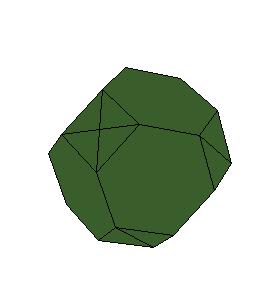
There are two ways to improve teaching of stereometry using computers. Moving 3-D graphics are allmost as good as real models in three-dimensional space. But the best way to learn about geometric models is to make them. Nets for models made by computer programs are more accurate then ruler amd compass constructions. In this paper we take truncated octahedron as an example.
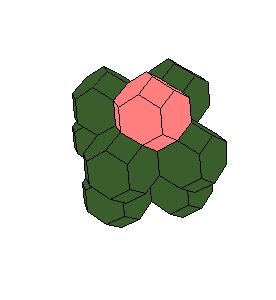
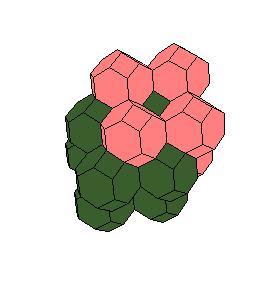
1. Truncated octahedra honeycomb three dimensions [5, pg. 167]. To invoke mathematica made animations click on picture [3].

| 
| 
|
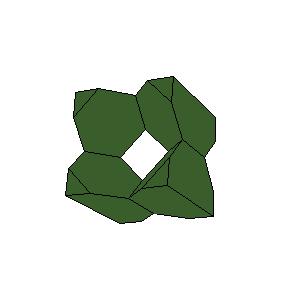
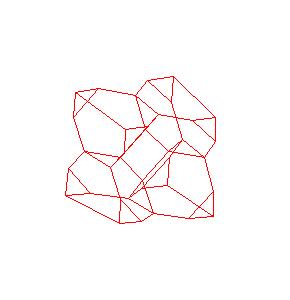
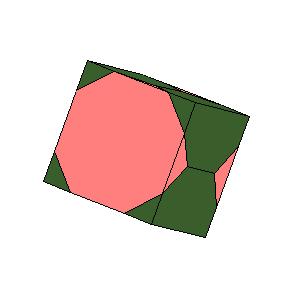
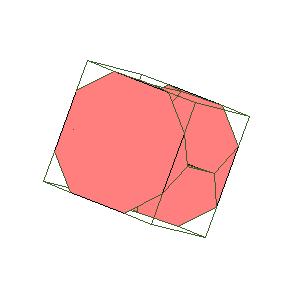
2. A direct consequence is a 6-piece dissection of two truncated octahedra to one cube. The dissection was noted by David Paterson and Anton Hanegraaf [1, pg. 249].
| 
| 
|
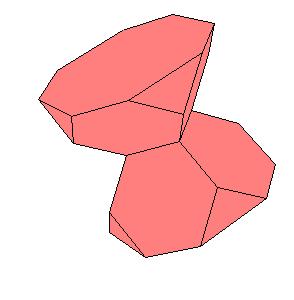
| 
| 
|
For dissection of one truncated octahedron to one cube see [1, pg. 241].
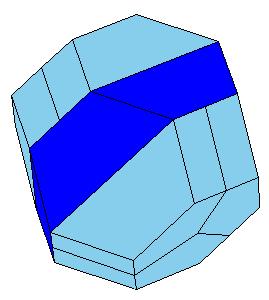
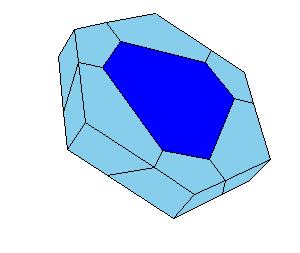
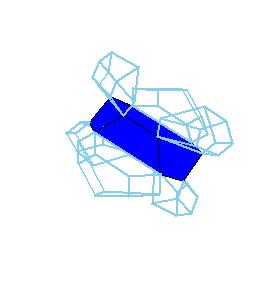
3. Anton Hanegraaf also found a hingeable dissection of a truncated octahedron to a hexagonal prism [2, pg. 201].
| 
|
| 
|
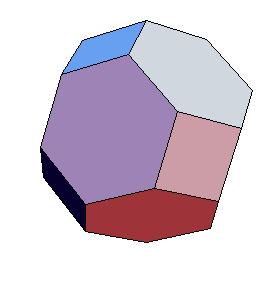
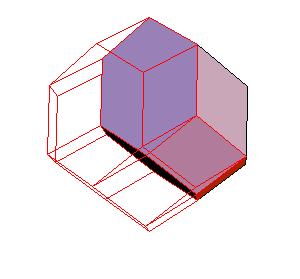
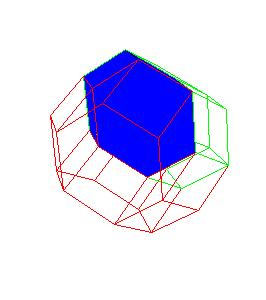
4. The truncated octahedron is an equilateral zonohedron [4]. So there is always a dissection of the solid to parallelepipeds (as was remarked by David Eppstein). Some parallelepipeds combine to hexagonal prisms.
| 
| 
|
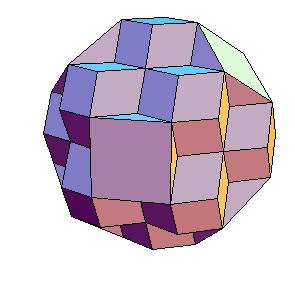
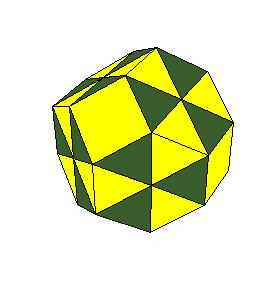
5. Rhombic dodecahedra also honeycomb three dimensions [5, pg. 168]. The truncated octahedron can be dissected to a combination of 16 rhombic dodecahedra (13 plus 6 halves).
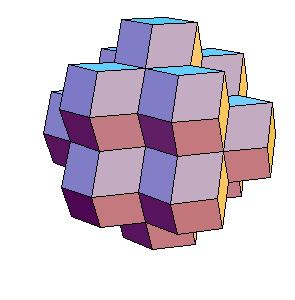
| 
| 
|
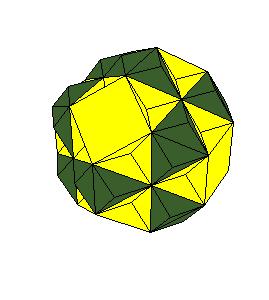
| 
| 
|
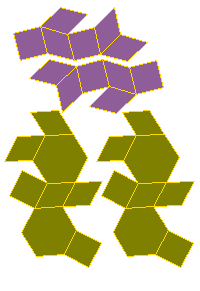
6. To make models use the following nets. Two copies of each will be needed.
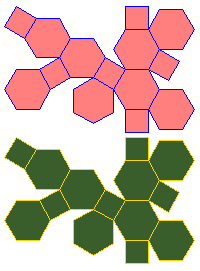
| 
|
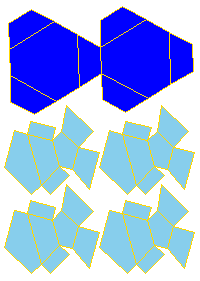
| 
|
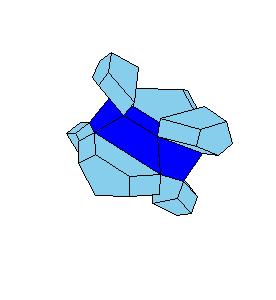
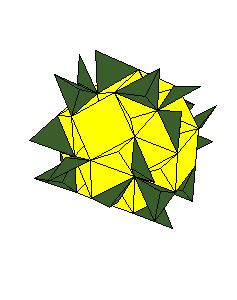
7. We made some models:

|

|

|
References
[1] G. Frederickson, Dissections: Plane & Fancy, Cambridge University Press, 1997 (hardcover) and 2003 (softcover).
[2] G. Frederickson, Hinged Dissections: Swinging & Twisting, Cambridge University Press, 2002 (hardcover).
[3] Martin Kraus' Live3D applet http://www.vis.uni-stuttgart.de/~kraus/index.html.
[4] Weisstein, Eric W. "Equilateral Zonohedron." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/EquilateralZonohedron.html
[5] R. Williams, The Geometrical Foundation Of Natural Structure, Dover 1972
Dr. Izidor Hafner is a lecturer of mathematics in the Faculty of electrical engineering of the University of Ljubljana, Slovenia. He is a coauthor of 12 text books of elementary mathematics and logic. He made scientific contribution in the theory of von Neumann regular rings, logic ang geometry.