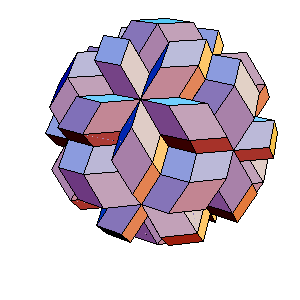
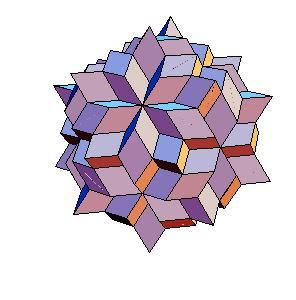
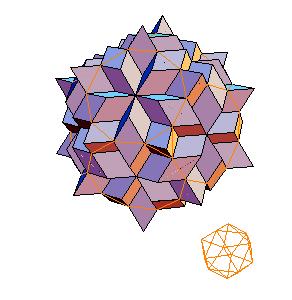
Abstract. Visual construction of a dissection of a rhombic solid to combination of the truncated dodecahedron and icosahedra is given.
The authors of [1, pg. 331] produced the table of the Dehn invariants for the non-snub unit edge Archimedean polyhedra. From this table the following combinations with sum 0 exist.
Truncated icosidodecahedron
Icosahedron + Truncated dodecahedron
Dodecahedron + Truncated icosahedron
Icosahedron + Dodecahedron + Icosidodecahedron
Icosidodecahedron + Rhombicosidodecahedron
Truncated icosahedron + Truncated dodecahedron + Rhombicosidodecahedron
For each of the above combinations we found an equidecomposable combination of rhombic solids [7]. By rhombic solid we mean a polyhedron that consists of prolate and oblate golden rhombohedra. In the solution we use also halves of rhombic dodecahedron of the second kind [4], which in turn consists of two rhombohedra.
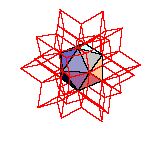
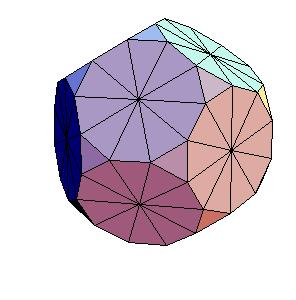
The dissection of a rhombic 210-hedron [6] to the combination of the truncated dodecahedron and the icosahedron is the most obvious one. Namely, if we cut off 20 spikes at the poles of triad symmetry, they form the icosahedron. The remaining concave and convex pyramidal forms at poles od pentad symmetry annihilate one another.

| 
| 
|
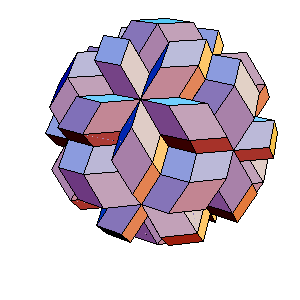
| 
| 
|
Subdivide the above 210-hedron and take away small rhombohedra at poles of triad axes. Remove 60 spikes at triad poles, use 20 to fill the gaps at poles and make 2 icosahedra (with the edge, that is a half of original one) from 40 remaining spikes.
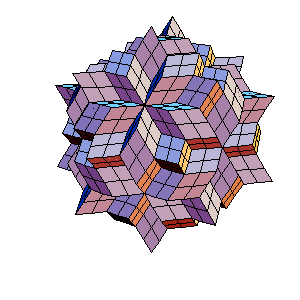
| 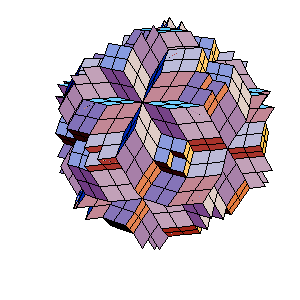
|
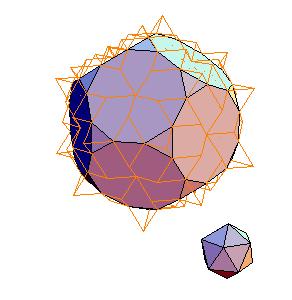
Continue the procces one step further, we get the truncated dodecahedron and 4 icosahedra (the edge being 1/4 of the origina).

| 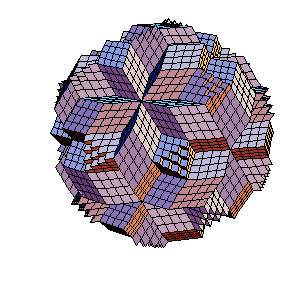
|
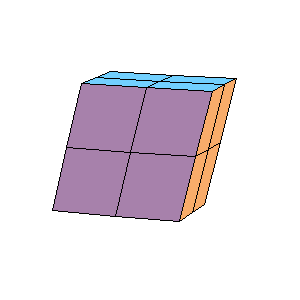
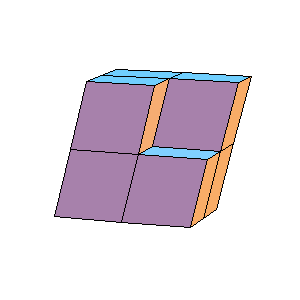
What is happening with rhombohedra at poles can be seen from the figures belove.

| 
| 
|
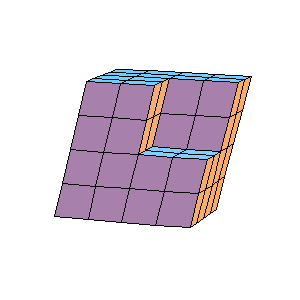
| 
| 
|

| 
| 
|
So next step will produce 8 icosahedra, then 16, ...
The proccess of adding and remowing rhombohedra at points of degee 3 can be caried out on whole surface. The result of the first step is given bolowe.
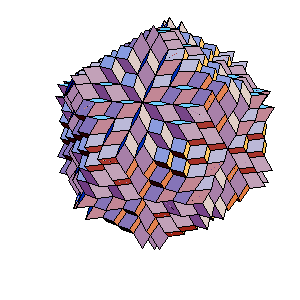
| 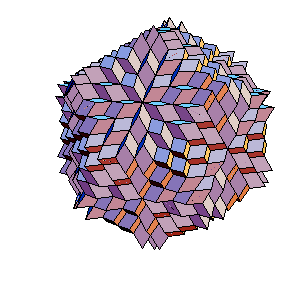
|
References
[1] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are
rational, Discrete & Computational Geometry, 22 (1999), pages 321-332.
[2] G. N. Frederickson, Dissections: Plane & Fancy, Cambridge U. Press, 1997.
[3] I. Hafner, T. Zitko, A dissection of quarter of rhombic dodecahedron of the second kind to a cube,
http://matematika.fe.uni-lj.si/people/izidor/homepage/RhombicPolyhedra/RhombicPolyhedra.html"
[4] I. Hafner, T. Zitko, Introduction to golden rhombic polyhedra
- published in Visual Mathematics Vol.4, No.2, 2002, 2, (3)
[5] I. Hafner, T. Zitko, Relations among rhombic, Platonic and Archimedean solids
- published in Visual Mathematics Vol.4, No.2, 2002, 2, (4)
[6] I. Hafner, B. Jurcic-Zlobec, T. Zitko, Gallery of rhombic polyhedra, - published in Visual Mathematics Vol.4, No.2, 2002, 2, (4)
[7] I. Hafner, Live3D Animation to Solution of Conway-Radin-Sadun problem, Visual Mathematics, Volume 9, No. 1, 2007 ,1
[8] Martin Kraus' Live3D applet http://www.vis.uni-stuttgart.de/~kraus/index.html.