The following combinations with sum 0 exist:
Truncated icosidodecahedron
Icosahedron+ Truncated dodecahedron
Dodecahedron+ Truncated icosahedron
Icosahedron+ Dodecahedron+ Icosidodecahedron
Icosidodecahedron+ Rhombicosidodecahedron
Truncated icosahedron+ Truncated dodecahedron+ Rhombicosidodecahedron
For each of the above combinations we found an equidecomposable combination of rhombic solids. In fact there are basically two solutions depending on the length of edges of the Archimedean solid, which may be shorter or larger diagonal of the rhombus.
1. Equidecomposable combinations, edge equals smaller diagonal
1. Icosahedron + dodecahedron + icosidodecahedron

| 
| 
|
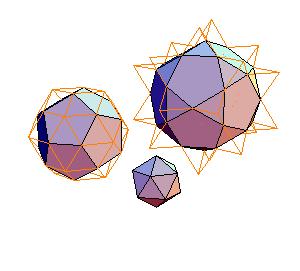
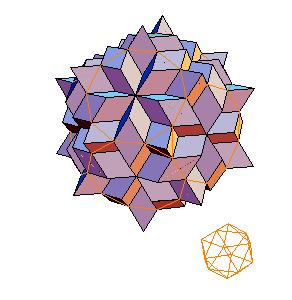
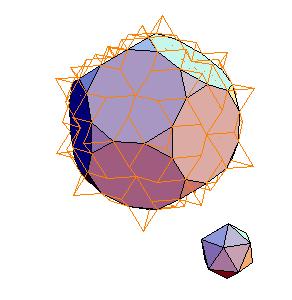
2. Icosahedron + truncated dodecahedron
| 
| 
|
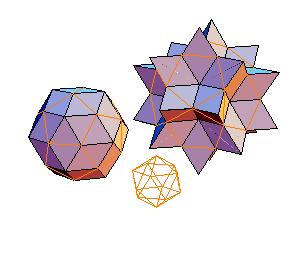
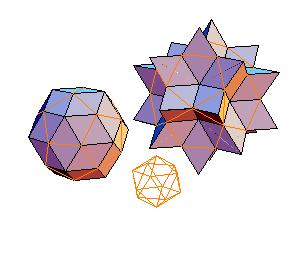
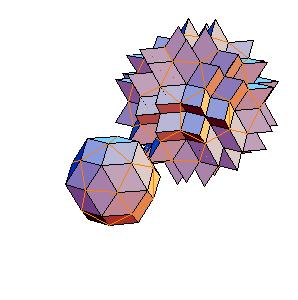
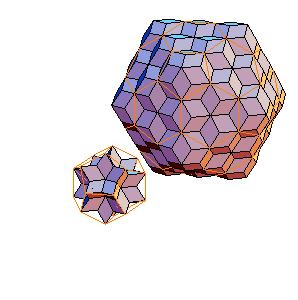
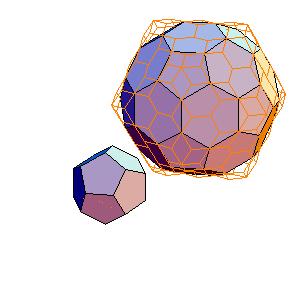
3. Dodecahedron + truncated icosahedron
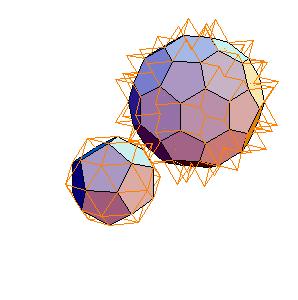
| 
| 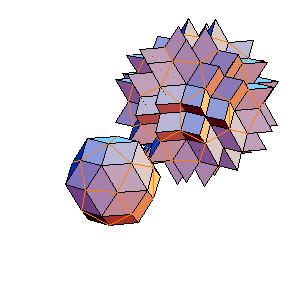
|
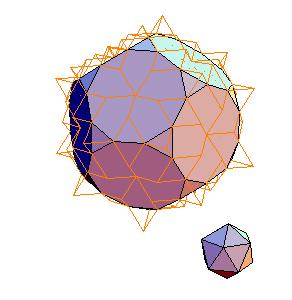
4. Icosidodecahedron + rhombicosidodecahedron
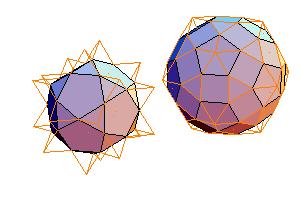
| 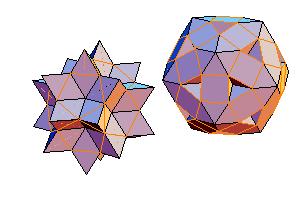
| 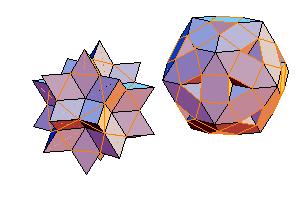
|
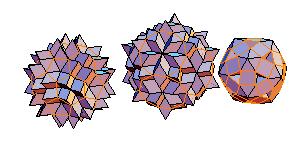
5. Truncated icosahedron + truncated dodecahedron + rhombicosidodecahedron
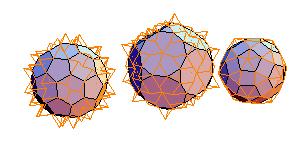
| 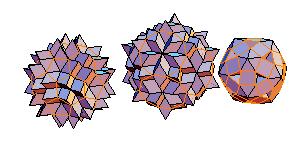
| 
|
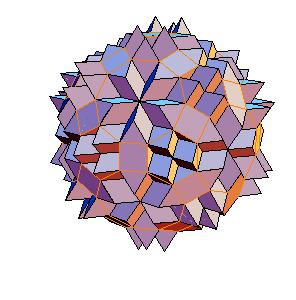
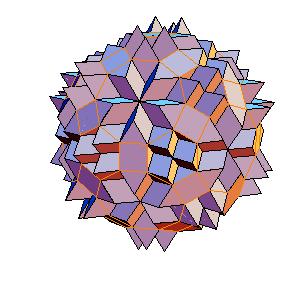
6. Truncated icosidodecahedron
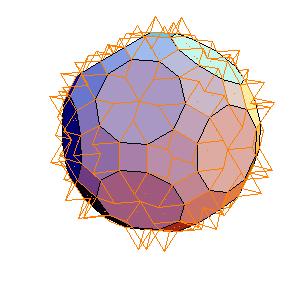
| 
| 
|
2. Equidecomposable combinations, edge equals larger diagonal
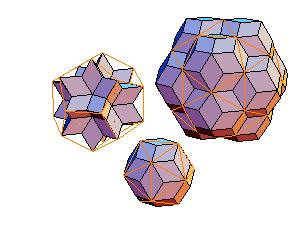
1. Icosahedron + dodecahedron + icosidodecahedron
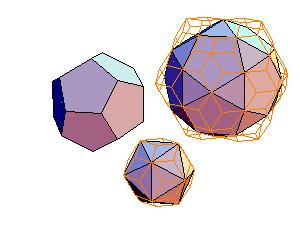
| 
| 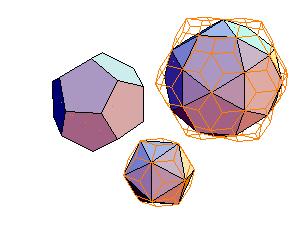
|
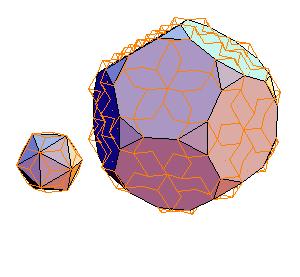
2. Icosahedron + truncated dodecahedron
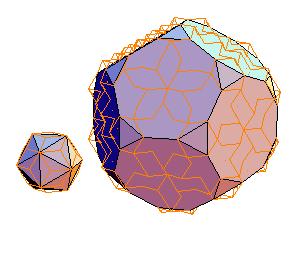
| 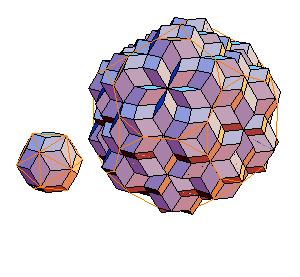
| 
|
3. Dodecahedron + truncated icosahedron
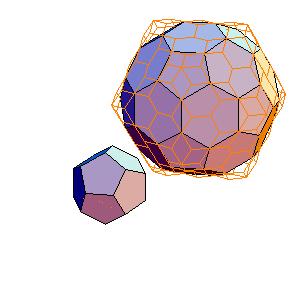
| 
| 
|
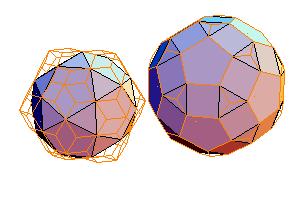
4. Icosidodecahedron + rhombicosidodecahedron
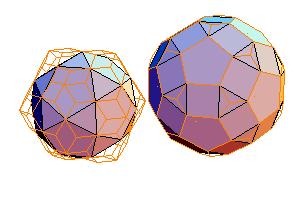
| 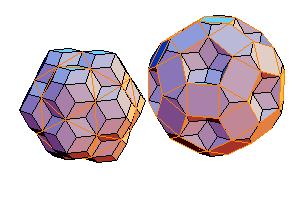
| 
|
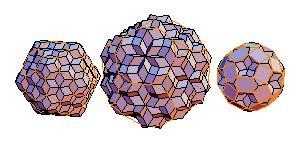
5. Truncated icosahedron + truncated dodecahedron + rhombicosidodecahedron
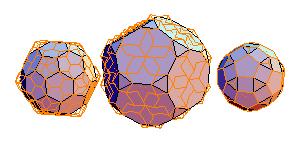
| 
| 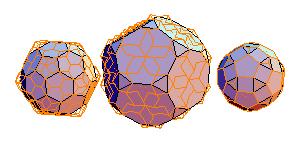
|
6. Truncated icosidodecahedron

| 
| 
|