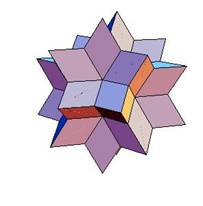
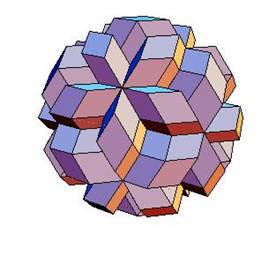
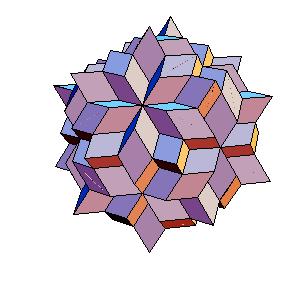
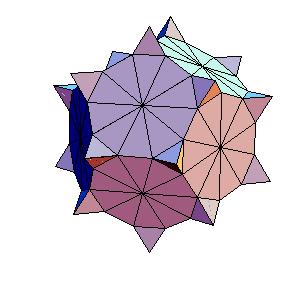
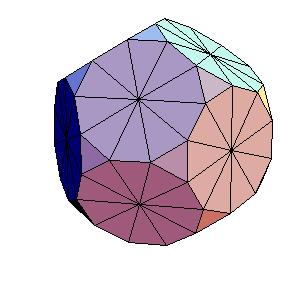
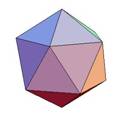
Dissection of rhombic 210-hedron to truncated dodecahedron and icosahedron

by Izidor Hafner

Faculty of Electrical Engineering, University of Ljubljana

Trzaska 25, 1000 Ljubljana, Slovenia

e-mail: izidor.hafner@fe.uni-lj.si

In [2] we have shown how to dissect icosahedron, dodecahedron, and icosidodecahedron to hexecontahedron and triacontahedron. In this way we answered Conway, Radin, Sadun problem [1, page 330]. Here is another example. Rhombic 210-hedron can be dissected to truncated dodecahedron and icosahedron. Rhombic 210-hedron consists of triacontahedron, 30 rhombic dodecahedra of the second kind and 20 prolate rhombohedra.

References

[1] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are

rational, Discrete & Computational Geometry, 22 (1999), pages 321-332.

[2] I. Hafner, Solution of Conway-Radin-Sadun Problem