Solution of Conway-Radin-Sadun Problem
By Izidor Hafner
Faculty of Electrical Engineering,
Trzaska 25 ,
1000
e-mail: izidor.hafner@fe.uni-lj.si
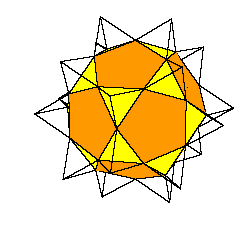
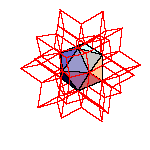
It was proved [1] that it is possible to dissect icosahedron, dodecahedron, and icosidodecahedron into finitely many pieces that can be reassembled to form a large cube. The authors admit that they have no idea how to perform such dissections. But the solution is quite simple. These solids can be dissected to rhombic triacontahedron and hexecontahedron. The first can be dissected to 10 prolate and 10 oblate rhombohedra and the second to 20 prolate rhombohedra. These prisms can be dissected into pieces and reassembled to a cube according to more or less standard procedure.
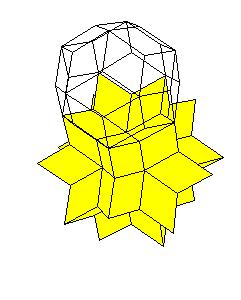
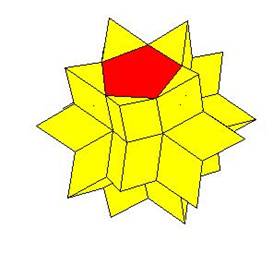
Te get the hexecontahedron and the triacontahedron on must dissect the icosahedron to 20 pyramids and put them on triangular faces of the icosidodecahedron; excavate 12 pentagonal pyramids from icosidodecahedron and put them on the dodecahedron.

References
[1] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are
rational, Discrete & Computational Geometry, 22 (1999), pages 321-332.