From dissection of the cube to space filling with prolate rhombohedra and rhombic dodecahedra of the second kind

Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25 , 1000 Ljubljana , Slovenia
e-mail: izidor.hafner@fe.uni-lj.si

Introduction.

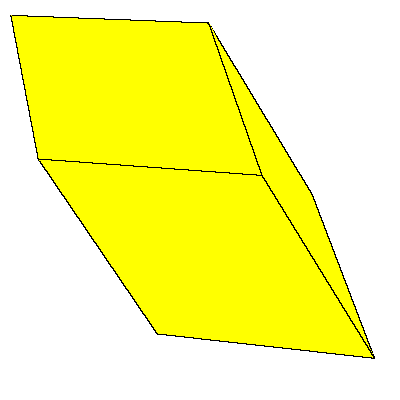
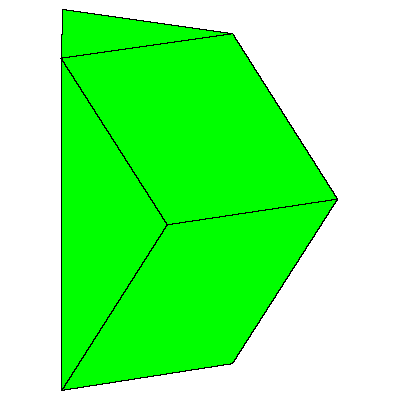
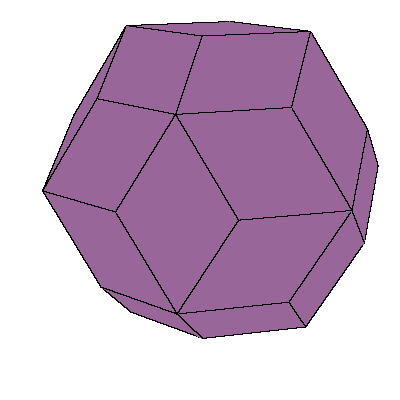
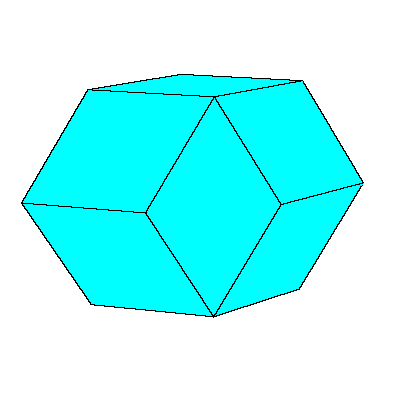
There is a family of isohedral rhombic polyhedra that consists of prolate and obtuse rhombohedron, (rhombic) dodecahedron of the second kind, discovered by Bilinski in 1960, rhombic icosahedron, discovered by Fedorov in 1885 and triacontahedron, discovered by Kepler in 1611 [1, p.156]. The faces of these solids are congruent rhombs whose diagonals are in golden ratio. The last three solids could be made by gluing appropriate number of rhombohedra. These five solids are the only convex polyhedra of this kind. See Introduction to golden rhombic polyhedra. The first three of the mentioned solids belong to so called five parallelohedra of Fedorov and can fill the space [2, p.165]. 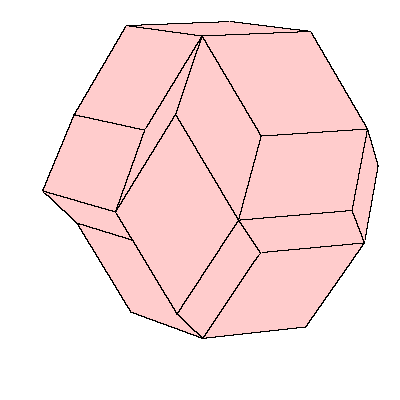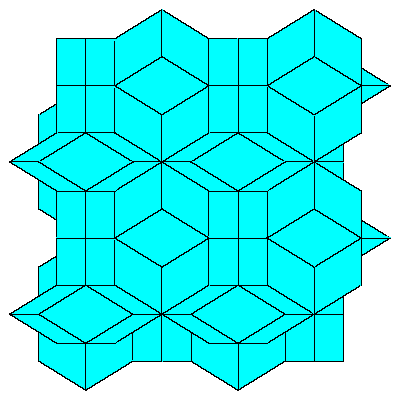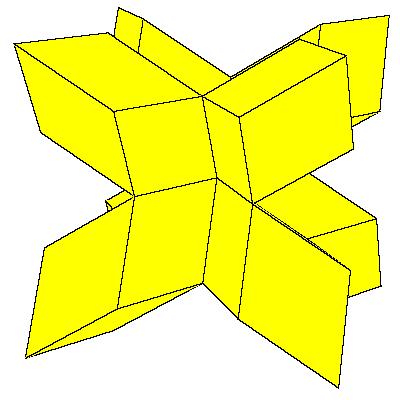In [2, pgs.195, 196] an open aggregation by triacontahedra is given. The intestices can be filled with a certain concave solid. The third figure below shows the solid and on the right of it there is the complementary aggregation. Our aim is to present an interesting filling of the space that uses prolate rhombohedron and (rhombic) dodecahedron. 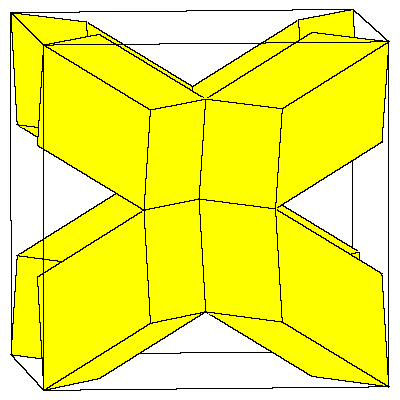The crucial element in the construction will be the rhombic hexecontahedron. We can made a model of it if we glue 20 prolate rhombohedra with common vertex. 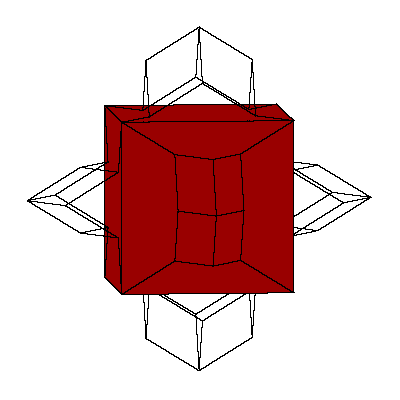We remove 12 rhombohedra in such way that the remaining solids form the cube. We can glue the dodecahedron to it in such a way that exactly a quarter of it lies in the cube. 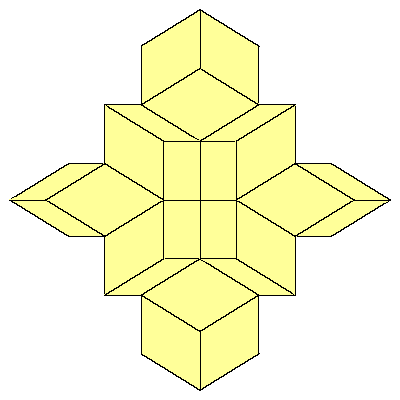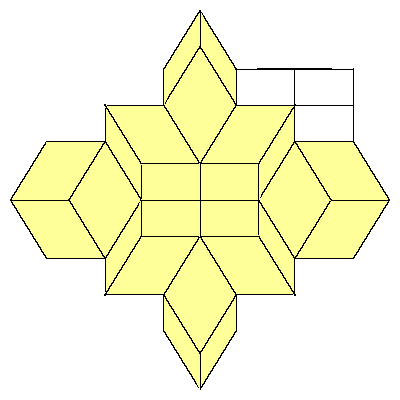We could also replace 12 rhombohedra with 6 rhombic dodecahedra. Exact half of each dodecahedron is inside the cube. If we look at the edges of the cube, we see that there is a space for a quarter of the dodecahedron. 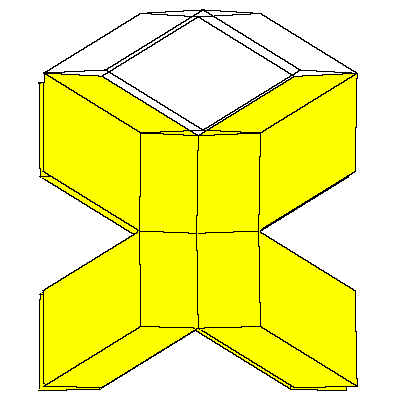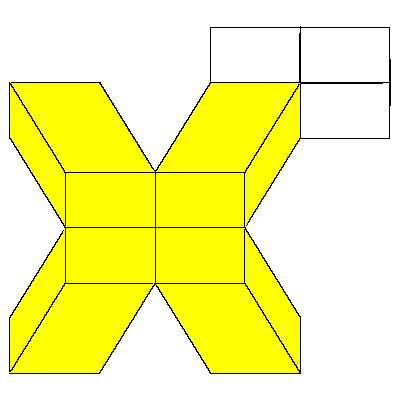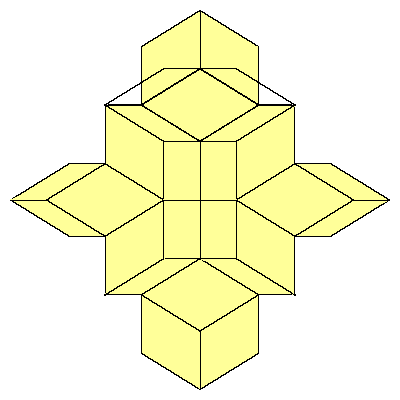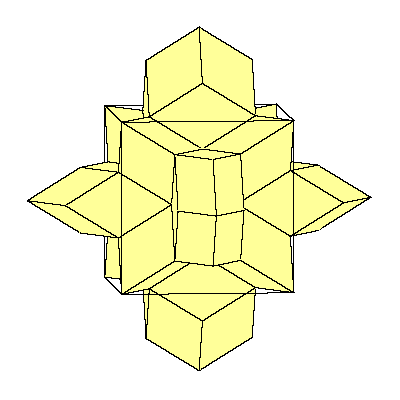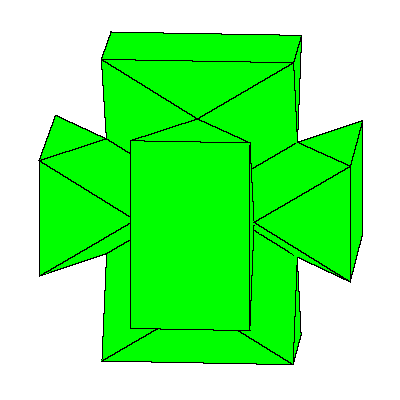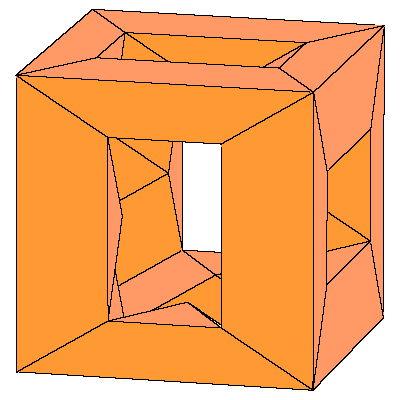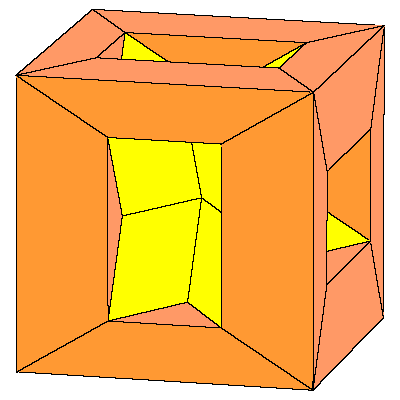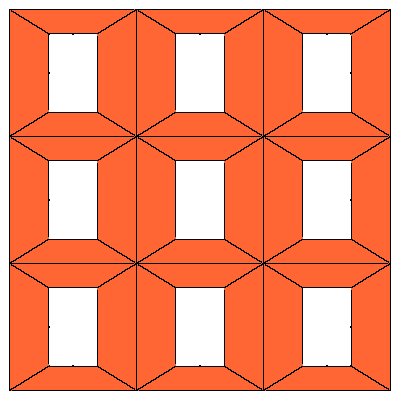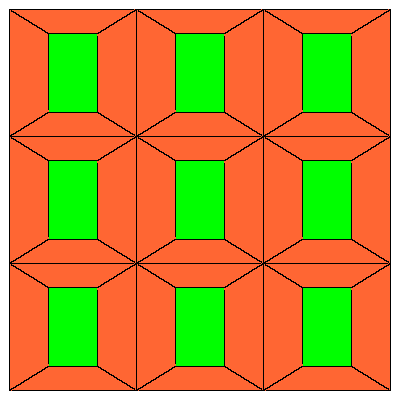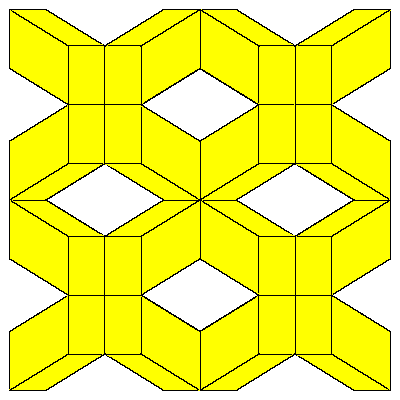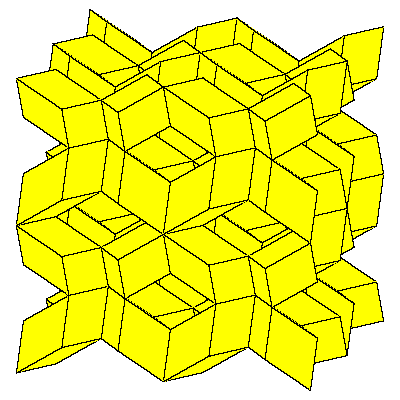So the cube can be decomposed into 8 prolate rhombohedra, 12 quarters and 6 halfs of the dodecahedron (so 6 dodecahedra all together). 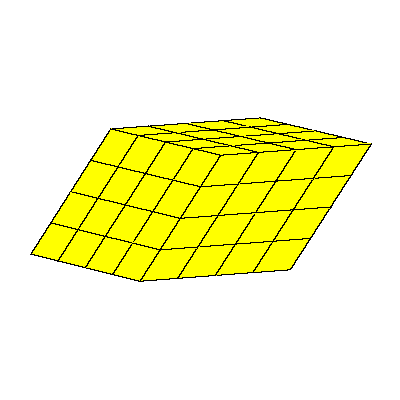The above mentioned decomposition of the cube is given below. 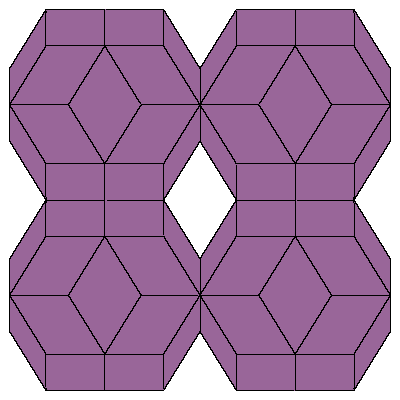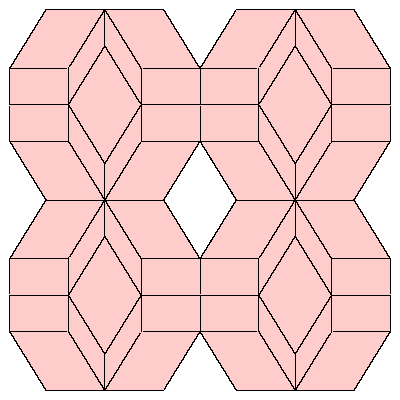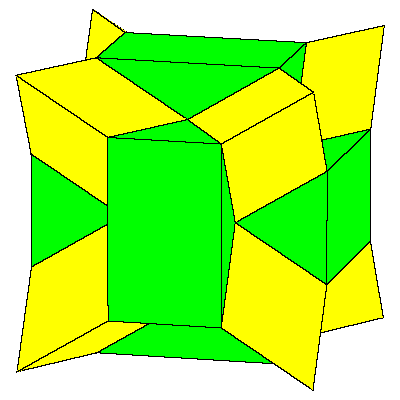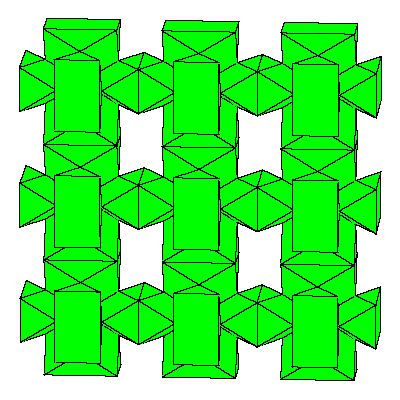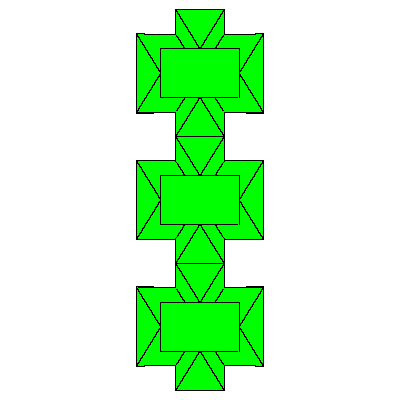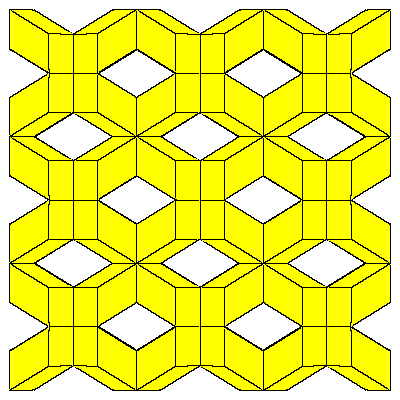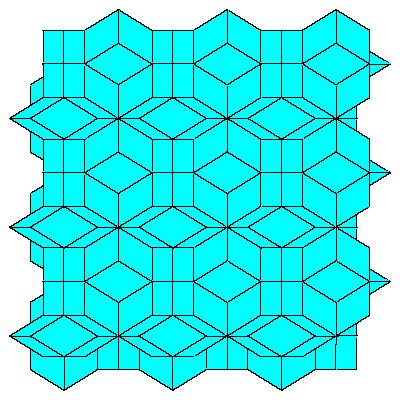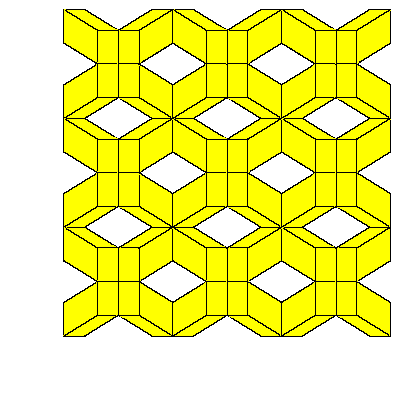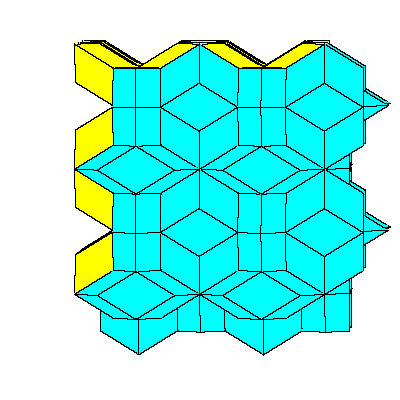Figures below represent one layer of space filling. To fill the space we do not need to decompose dodecahedra. We only need to take 6 of them in special combination.

References

[1] P. R. Cromwell, Polyhedra, Cambridge U. Pr., 1997
[2] R. Williams, The Geometrical Foundation of Natural Structure, Dover Publication, Inc, New York, 1972
[3] Tohru Ogawa, An essentially-three-dimensional quasicrystals, http://members.tripod.com/vismath2/ogawa/es.htm
[4] Tohru Ogawa, Symmetry of three-dimensional quasicrystals, http://members.tripod.com/vismath2/ogawa/3d.htm
[5] George Hart, Johannes Kepler's Polyhedra, http://www.georgehart.com/virtual-polyhedra/kepler.html