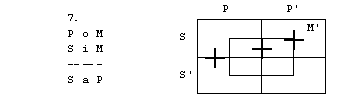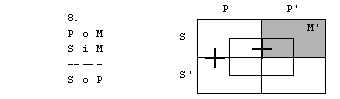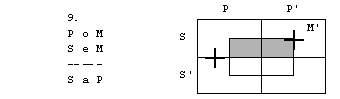Tradicionalni račun imen

Tako imenujem logiko imen ali terminov, ki jo je razvil Grški filozof Aristotel, sicer tudi učitelj Aleksandra Makedonskega. Račun imen proučuje odnose med t.i. kategoričnimi stavki. Te delimo na:

1) splošno trdilne, ki imajo obliko »Vsak S je P.«

2) delno trdilne, ki imajo obliko »Vsaj en S je P.« (Nekateri S so P.)

3) splošno nikalne, ki imajo obliko »Noben S ni P.« (Ne obstaja S, ki je P.)

4) delno nikalne, ki imajo obliko »Vsaj en S ni P.« (Nekateri S niso P.)

Imeni ali termina S in P imenujem subjekt in predikat stavka.

V računu imen se uporabljajo naslednji zapisi kategoričnih stavkov:

S a P º Vsak S je P.

S i P º Vsaj en S je P.

S e P º Noben S ni P.

S o P º Vsaj en S ni P.

Glede na pomene stavkov lahko njihovo resničnost ponazorimo z diagrami. Najbolj znani so Vennovi diagrami, vendar se bomo tokrat poslužili Carollovih diagramov.

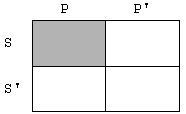
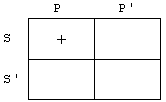
Pogovorno področje, to je množico vseh reči o katerih se pogovarjamo, razdelimo na štiri dele. Prvi del predstavlja tiste reči, ki imajo tako lastnost S kot P. Drugi del so tisti, ki imajo lastnost S nimajo pa lastnosti P. Oznaka P’ je oznaka za komplement ali negacijo imena P. Tretji del so reči, ki niso S, so pa P, in četrti tiste reči, ki niso ne S ne P.

Osenčeno področje pomeni, da tam ni nobene reči. V našem primeru ne obstaja S, ki bi bil P. To, da obstaja S, ki je P, zaznamujemo s + .

Zadnji diagram pove, da obstaja vsaj en S (ne vemo pa ali je P ali P’). Glede na dogovorjeno, lahko resničnost in neresničnost kategoričnih stavkov predstavimo s tamelo.

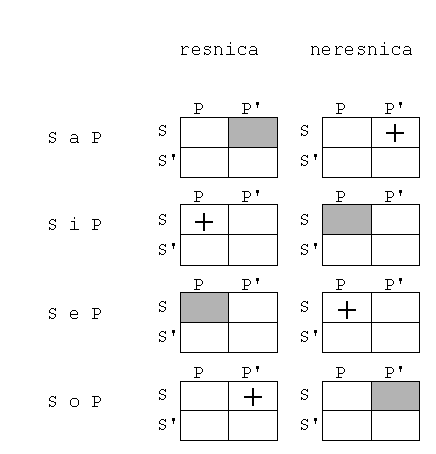
Iz tabele razberemo, da sta stavka S a P in S o P kontradiktorna (nasprotujoča), to je kadar je eden resničen, je drugi neresničen. Enako velja za stavka S i P in S e P. Seveda tudi brez diagrama lahko ugotovimo, da so negacije stavkov:

Vsak S je P	Obstaja S, ki ni P
Vsaj en S je P	Noben S ni P
Noben S ni P	Vsaj en S je P
Vsaj en S ni P	Vsak S je P

To, da področje X ni prazno, lahko definiramo:

Ex(X) º X i X.

Silogizmi

Silogizmi so pravila sklepanja, v katerih iz dveh kategoričnih stavkov (predpostavk ali premis) logično sledi tretji kategorični stavek (zaključek ali sklep).

Nekateri silogizmi potrebujejo še predpostavko, da neko področje ni prazno.

Sklep ima obliko S x P, S je subljek in P predikat. Prva predpostavka ima obliko P y M ali M y P, druga pa S z M ali M z S. Termin M nastopa v obeh predpostavkah se imenuje srednji termin. Terminoma S in P pa rečemo nižji in višji termin. Tudi premisama rečemo višja in nižja premisa.

Glede na položaj srednjega termina razlikujemo štiri silogistične figure.

I II III IV

M P P M M P P M

S M S M M S M S

------- ------ ------- -------

S P S P S P S P

V vsaki figuri lahko postavimo a, i, e in o v tri stavke silogizma. To pomeni, da imamo v vsaki figure 4.4.4=64 silogizmov. Tako je skupaj 256 silogizmov, vendar je le 24 logično pravilnih, 9 od the potrebujejo še predpostavko o nepraznosti območja.

1. figura

Kako ugotovimo pravilnost oz. nepravilnost silogizma?

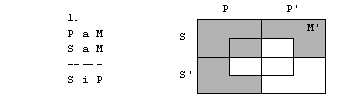
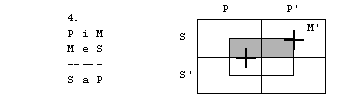
Oglejmo si silogizem

M e P

S a M

S e P

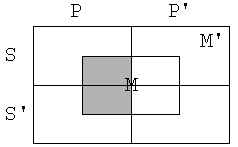
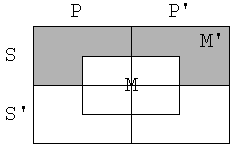
Naj prej moramo diagrame razširiti še za M in M’.

Reči z lastnostjo M predstavljajo točke, ki so blizi sredine, točke proti robu pa predstavljajo reči, ki nimajo lastnosti M. Tako je podovorno področje podedeljeno na 8 delov.

To, da noben M ni P označimo tako, da osenčimo (izpraznimo) tiste M, ki so v P.

Pravilnot silogizma pomeni, da ni možno, da sta premisi resnični, zaključek pa neresničen.

Negacija zaključka S e P, to je, da noben S ni P, je obstaja S, ki je P, to je S i P. Na področje SP postavimo +.

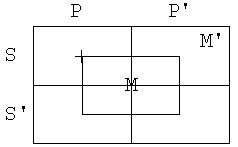
Zdaj zberemo vse tri diagrame skupaj

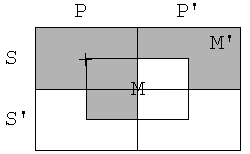
Diagram hkrati zahteva, da področje SP ni prazno (+) in da je prezno (osenčenje). To je seveda protislovje. Zato je silogizem pravilen.

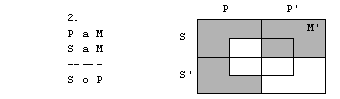
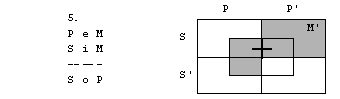
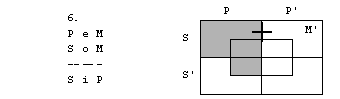
Oglejmo si silogizem

P e M

S i M

S o P

Negacija stavka S o P, to je obstaja S, ki ni P, je vsak S je P.

Narišimo diagrame za premise in negacijo zaključka.

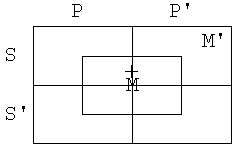
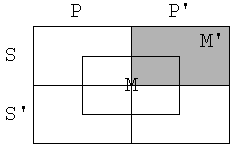
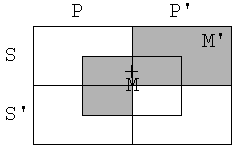
Tudi tokrat je protislovnost premis in negacije zaključka. Silogizem je pravilen.

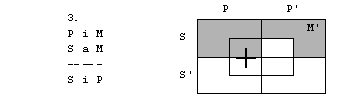
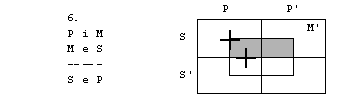
Vzemimo zdaj silogizem

P e M

M e S

S e P

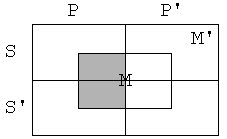
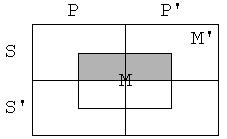
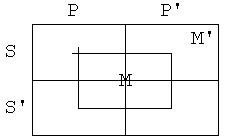
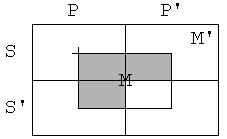
Tokrat diagram ne predstavlja protislovne situacije. Možno je, da sta premisi resnični, zaključek pa napačen, oz. negacija zaključka resnična. Taki situaciji rečemo protiprimer.

Če imamo reč z lastnostmi S, P in M’, sta premisi izpolnjeni, zaključek pa ni.

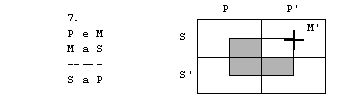
Oglejmo si primer silogizma

Vsak delfin je sesalec.

Nobena riba ni delfin.

Nobena riba ni sesalec.

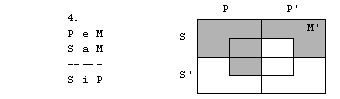
Tu so vsi trije stavki resnični. Vendar pa tretji stavek ne sledi logično iz prvih dveh. Če bi logično sledil, bi bil silogizem

M a P

S e M

S e P

pravilen. Da pa ni, je razvidno iz naslednjih diagramov.

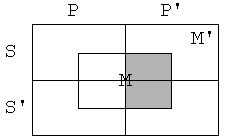
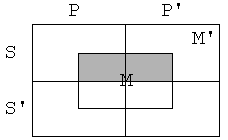
To pa ni protislovje. Če obstaja reč, ki je S, P in ni M, sta premisi resnični, zaključek pa napačen. Silogizem ni pravilen.

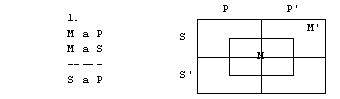
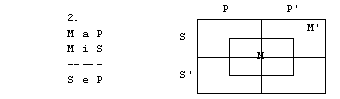
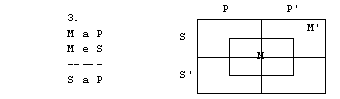
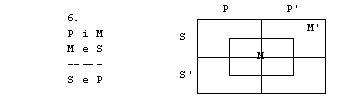
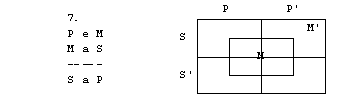
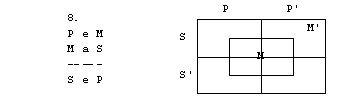
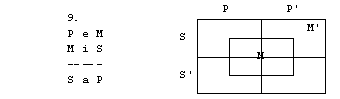
Naloge

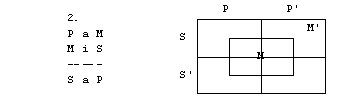
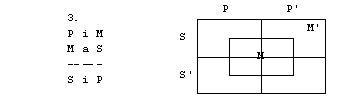
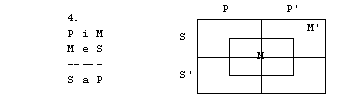
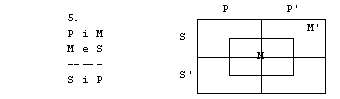
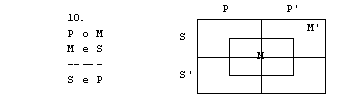
1. S pomočjo diagramov določi pravilnost oz. nepravilnost silogizmov.

1. figura

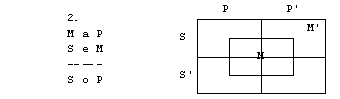
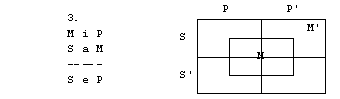
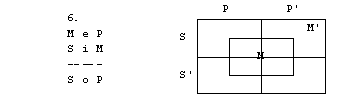
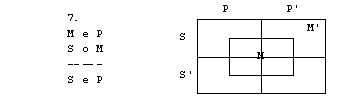
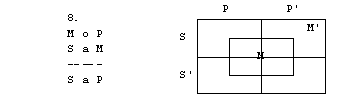
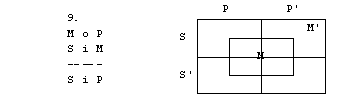
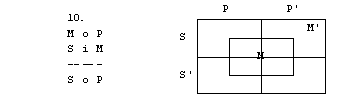
2. figura

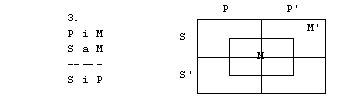
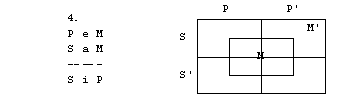
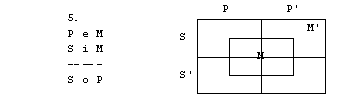
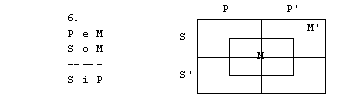
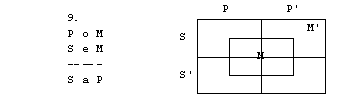
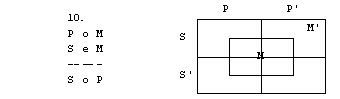
3. figura

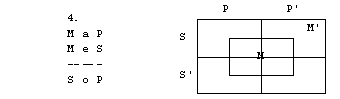
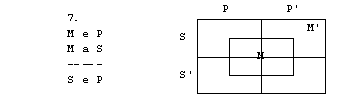
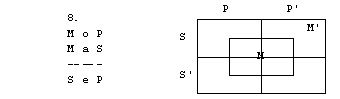
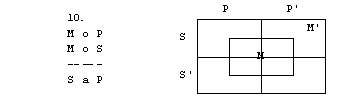
4. figura

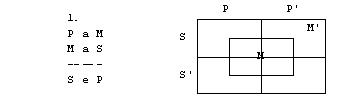
2. V naslednjih stavkih določi termine silogizmov in z diagrami določi pravilnost oz. nepravilnost.

1. figura

1. Vsak lik v srednjem delu je lik na levi strani.Vsak lik v zgornjem delu je lik v srednjem delu.Vsaj en lik v zgornjem delu je lik na levi strani.

2. Vsaj en lik v srednjem delu je lik na levi strani.Vsaj en lik v zgornjem delu je lik v srednjem delu.Vsaj en lik v zgornjem delu je lik na levi strani.

3. Vsaj en lik v srednjem delu je lik na levi strani.Vsaj en lik v zgornjem delu je lik v srednjem delu.Vsaj en lik v zgornjem delu ni lik na levi strani.

2. figura

1. Vsak lik na levi strani je lik v srednjem delu.Vsaj en lik v zgornjem delu ni lik v srednjem delu.Vsaj en lik v zgornjem delu ni lik na levi strani.

2. Vsaj en lik na levi strani je lik v srednjem delu.Vsaj en lik v zgornjem delu je lik v srednjem delu.Vsaj en lik v zgornjem delu ni lik na levi strani.

3. Noben lik na levi strani ni lik v srednjem delu.Vsak lik v zgornjem delu je lik v srednjem delu.Vsak lik v zgornjem delu je lik na levi strani.

3. figura

1. Vsaj en lik v srednjem delu je lik na levi strani.Vsaj en lik v srednjem delu ni lik v zgornjem delu.Noben lik v zgornjem delu ni lik na levi strani.

2. Vsaj en lik v srednjem delu je lik na levi strani.Vsaj en lik v srednjem delu ni lik v zgornjem delu.Vsaj en lik v zgornjem delu ni lik na levi strani.

3. Noben lik v srednjem delu ni lik na levi strani.Noben lik v srednjem delu ni lik v zgornjem delu.Vsaj en lik v zgornjem delu ni lik na levi strani.

4. figura

1. Vsak lik na levi strani je lik v srednjem delu.Vsaj en lik v srednjem delu ni lik v zgornjem delu.Vsak lik v zgornjem delu je lik na levi strani.

2. Vsaj en lik na levi strani je lik v srednjem delu.Vsak lik v srednjem delu je lik v zgornjem delu.Vsaj en lik v zgornjem delu je lik na levi strani.

3. Vsaj en lik na levi strani je lik v srednjem delu.Noben lik v srednjem delu ni lik v zgornjem delu.Noben lik v zgornjem delu ni lik na levi strani.

Rešitve: 1. naloga

1. figura

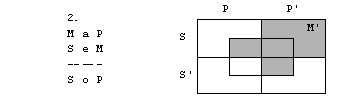
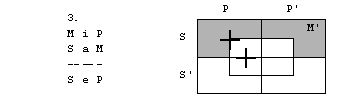
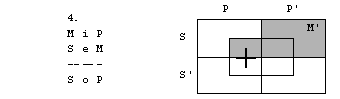
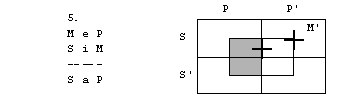
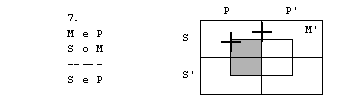
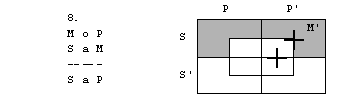
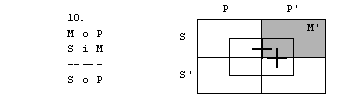
2. figura

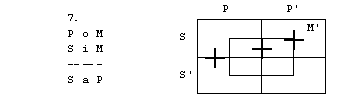
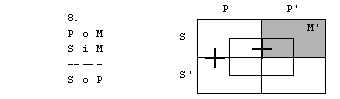
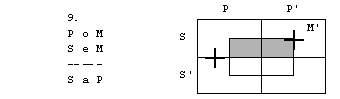
3. figura

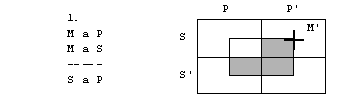
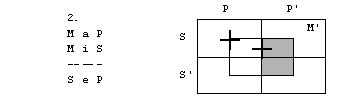
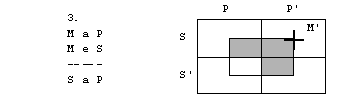
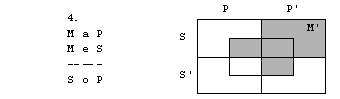
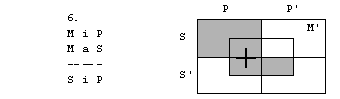
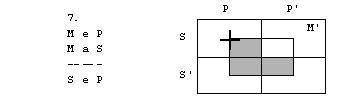
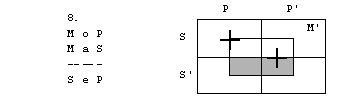
4. figura

2. naloga

1. figura

1. P, 2. N, 3. N.

2. figura

1. N, 2. N, 3. N.

3. figura

1. N, 2. N, 3. N.

4. figura

1. N, 2. N, 3. N.

Izidor Hafner