Two convex polyhedra with a common net

Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25 , 1000 Ljubljana , Slovenia
e-mail: izidor.hafner@fe.uni-lj.si

In the article Rigidity of convex polyhedrons by N. P. Dolbilin (Quantum, September/October 1998, pgs.8-13) we learnt about Alexandrov's sufficiency theorem about developments that produce convex polyhedra. A development is a set of polygons and rules that note which sides should be glued together. On the other hand a net of a polyhedron is a single plane polygon obtained by cutting the polyhedron along edges. An example of a net that can be glued into two different convex polyhedra is given.

By golden octahedron we mean a bipyramid, where the pyramid has golden rectangle as its basis and two equilateral and two isosceles triangles as the side faces.

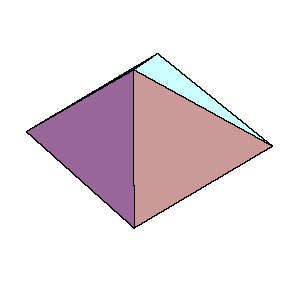
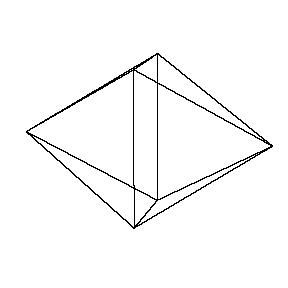
The next figure is a net of the golden octahedron.

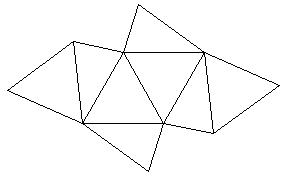
But this net is also a net of another polyhedron.

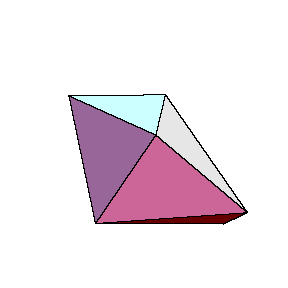
The polyhedron could be described as the regular tetrahedron augmented by two congruent (non)regular tetrahedra.

Animations