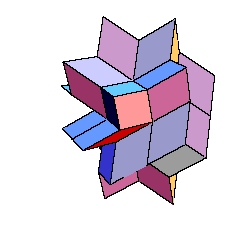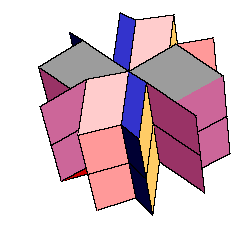Construction of rhombic hexecontahedra
Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25
, 1000 Ljubljana
, Slovenia
e-mail: izidor.hafner@fe.uni-lj.si
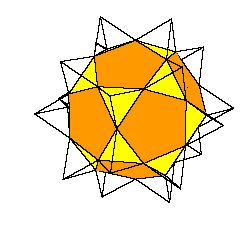
The hexecontahedron is a solid that consists of 20 prolate golden rhombohedra. The solid has icosahedral symmetry.
In [3]
the solid is called flower dodecahedron. Some of its relations to Platonic and Archimedean solids are shown in [2]. It is also known that two oblate rhombohedra and two obtuse rhombohedra form the rhombic dodecahedron of the second kind. The space angle of two prolate rhombohedra stacked together at vertex of smaller space angle is 1/10 of full space angle and the same is true for two oblate rhombohedra
[3].
So we could replace two adjacent prolate rhombohedra by pair of obtuse rhombohedra. The problem is to find all different ways to do it. The new solids also have 60 faces, but the symmetry is lost.
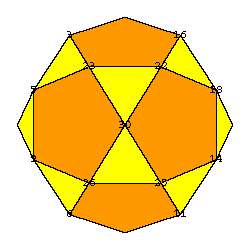
Each adjacent pair of prolate rhombohedra are stacked along an axis of twofold symmetry. To such a pair there coresponds a vertex of an icosidodecahedron. Suppose we replace a pair of prolate rhombohedra that corresponds to a vertex of the icosidodecahedron. The point that corresponds to another such pair can not be adjacent to the first point. This means that points that correspond to replaced pairs form an independent set in the graph of the icosidodecahedron.
So the problem is to find all independent sets. The number of elements of an independent set is evidently between 0 and 10. The original hexecontahedron corresponds to 0 and there is essentially only one possibility for the first replacement.
So we could always fix the first vertex, in our case it will be 30.
To eliminate essentialy equal independent sets we shall need a subgroup that fixes vertex 30. The subgroup has 2 elements and this subgroup acts as a group on 25 vertices. (We delete vertex 30 and adjacent vertices 22,23,25,26.) As soon as an independent set is generated, we make its orbit space and eliminate other sets in the orbit. Checking independence is a routine in mathematica (add-ons, combinatorica)and the code that deals with groups is adopted from [1]. Once all different independent sets are found we wish to classify them according their degree of symmetry. This means that we are looking for a maximal subgroup of the icosahedral group that leaves a given independent set invariant.
The next table presents the results.
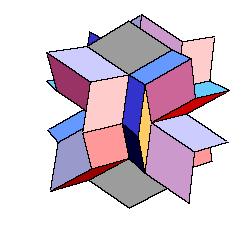
To each hexecontahedron there corresponds a space filling. Here are 5 examples.
[1] J. W. Gray, Mastering Mathematica, Second edition, Academic Press, London 1998
[2] I. Hafner, T. Zitko, Relations among rhombic, Platonic and Archimedean solids, (submitted)
[3]
Tohru Ogawa, Symmetry of three-dimensional quasicrystals,