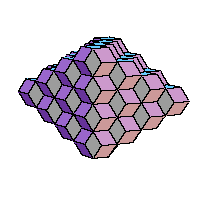
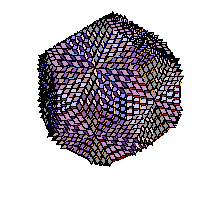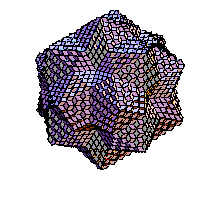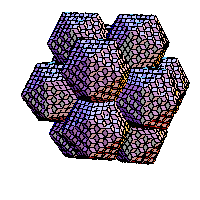Families of golden rhombic polyhedra

Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25 , 1000 Ljubljana , Slovenia
e-mail: izidor.hafner@fe.uni-lj.si

By alternation of two operations on a rhombic solid a family of rhombic solids is obtained. Such a family has sometimes as a limit well known solid (icosahedron, truncated dodecahedron). The first operation is subdivision. If we look at it as an operation on the surface of a solid it subdivides each face (golden rhombus) into four congruent smaller faces. If we look at a solid as composed of prolate and obtuse rhombohedra, subdivision cuts each rhombohedron into eight congruent rhombohedra. The second operation is an inversion. In the case of a convex vertex of degree three it cuts in the rhombohedron whose three faces are adjacent to the vertex. In case of a concave vertex of degree three it adds a rhombohedron whose faces are adjacent to the vertex. We applied these transformations on some solid from Gallery of Rhombic Polyhedra, Visual Mathematics, #1, 2002, 4.