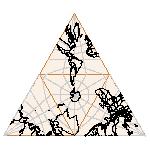
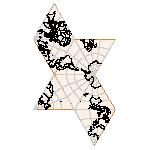
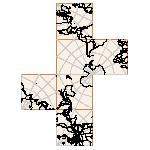
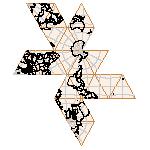
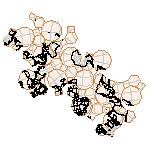
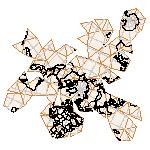
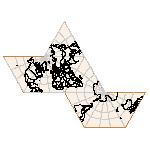
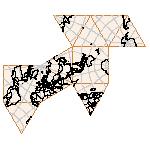
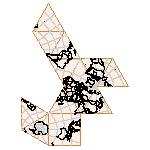
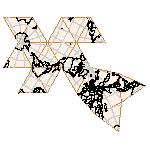
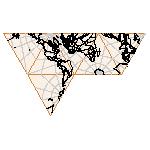
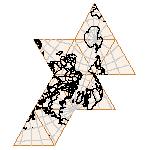
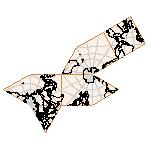
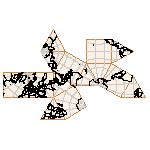
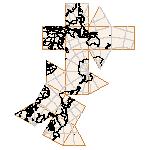
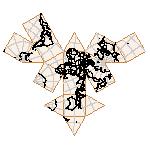
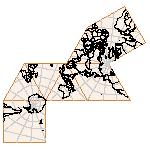
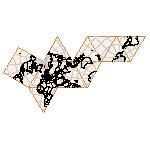
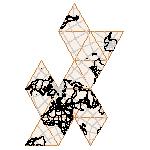
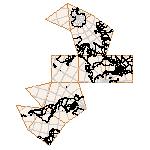
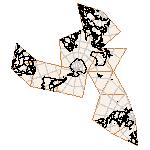
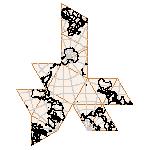
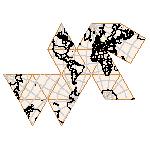
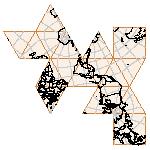
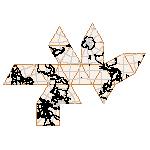
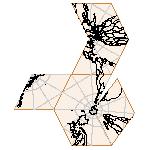
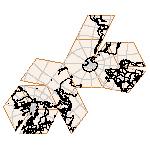
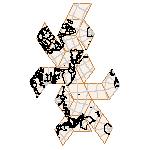
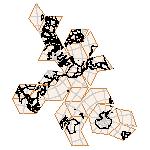
Maps on random polyhedra nets are generated by mathematica computer program: Platonic solids, Archimedean solids, antiprisms, prisms, Johnson's solids, rhombic solids, Catalan solids.
In the chapter Curious Maps (Gardner, M. (1988), Time Travel, W.H. Freeman and Company, New York, pg.196), many world's maps are presented, some of them use a projection on a convex solid, that is unfolded into a plane net. »The mathematician Charles Sanders Peirce designed a conformal map, namely a projection on eight isosceles right triangles that may be regarded as the faces of an octahedron, flattened until a space diagonal is zero. B.J.S. Cahill patented his butterfly map in 1913. The world is projected onto a regular octahedron. R. Buckminster Fuller's first Dymaxion map was a projection of the world onto the fourteen faces of a cuboctahedron. In March 1, 1943 the map was completed by staff artists of Life. At about the same time, Irving Fisher designed Likaglobe, which folds into an icosahedron. In 1954 Fuller copyrighted his Dymaxion Skyocean Projection World Map, which slightly differed from Fisher's Likaglobe.«
Click on a figure to get a larger one.